Physical systems are divided into types according to their unchanging (or ‘state-independent’) properties, and the state of a system at a time consists of a complete specification of those of its properties that change with time (its ‘state-dependent’ properties). To give a complete description of a system, then, we need to say what type of system it is and what its state is at each moment in its history.
A physical quantity is a mutually exclusive and jointly exhaustive family of physical properties (for those who know this way of talking, it is a family of properties with the structure of the cells in a partition). Knowing what kinds of values a quantity takes can tell us a great deal about the relations among the properties of which it is composed. The values of a bivalent quantity, for instance, form a set with two members; the values of a real-valued quantity form a set with the structure of the real numbers. This is a special case of something we will see again and again, viz., that knowing what kind of mathematical objects represent the elements in some set (here, the values of a physical quantity; later, the states that a system can assume, or the quantities pertaining to it) tells us a very great deal (indeed, arguably, all there is to know) about the relations among them.
In quantum mechanical contexts, the term ‘observable’ is used interchangeably with ‘physical quantity’, and should be treated as a technical term with the same meaning. It is no accident that the early developers of the theory chose the term, but the choice was made for reasons that are not, nowadays, generally accepted. The state-space of a system is the space formed by the set of its possible states,[2] i.e., the physically possible ways of combining the values of quantities that characterize it internally. In classical theories, a set of quantities which forms a supervenience basis for the rest is typically designated as ‘basic’ or ‘fundamental’, and, since any mathematically possible way of combining their values is a physical possibility, the state-space can be obtained by simply taking these as coordinates.[3] So, for instance, the state-space of a classical mechanical system composed of n particles, obtained by specifying the values of 6n real-valued quantities - three components of position, and three of momentum for each particle in the system - is a 6n-dimensional coordinate space. Each possible state of such a system corresponds to a point in the space, and each point in the space corresponds to a possible state of such a system. The situation is a little different in quantum mechanics, where there are mathematically describable ways of combining the values of the quantities that don't represent physically possible states. As we will see, the state-spaces of quantum mechanics are special kinds of vector spaces, known as Hilbert spaces, and they have more internal structure than their classical counterparts.
A structure is a set of elements on which certain operations and relations are defined, a mathematical structure is just a structure in which the elements are mathematical objects (numbers, sets, vectors) and the operations mathematical ones, and a model is a mathematical structure used to represent some physically significant structure in the world.
The heart and soul of quantum mechanics is contained in the Hilbert spaces that represent the state-spaces of quantum mechanical systems. The internal relations among states and quantities, and everything this entails about the ways quantum mechanical systems behave, are all woven into the structure of these spaces, embodied in the relations among the mathematical objects which represent them.[4] This means that understanding what a system is like according to quantum mechanics is inseparable from familiarity with the internal structure of those spaces. Know your way around Hilbert space, and become familiar with the dynamical laws that describe the paths that vectors travel through it, and you know everything there is to know, in the terms provided by the theory, about the systems that it describes.
By ‘know your way around’ Hilbert space, I mean something more than possess a description or a map of it; anybody who has a quantum mechanics textbook on their shelf has that. I mean know your way around it in the way you know your way around the city in which you live. This is a practical kind of knowledge that comes in degrees and it is best acquired by learning to solve problems of the form: How do I get from A to B? Can I get there without passing through C? And what is the shortest route? Graduate students in physics spend long years gaining familiarity with the nooks and crannies of Hilbert space, locating familiar landmarks, treading its beaten paths, learning where secret passages and dead ends lie, and developing a sense of the overall lay of the land. They learn how to navigate Hilbert space in the way a cab driver learns to navigate his city.
How much of this kind of knowledge is needed to approach the philosophical problems associated with the theory? In the beginning, not very much: just the most general facts about the geometry of the landscape (which is, in any case, unlike that of most cities, beautifully organized), and the paths that (the vectors representing the states of) systems travel through them. That is what will be introduced here: first a bit of easy math, and then, in a nutshell, the theory.
Vectors and vector spaces
A vector A, written ‘|A>’, is a mathematical object characterized by a length, |A|, and a direction. A normalized vector is a vector of length 1; i.e., |A| = 1. Vectors can be added together, multiplied by constants (including complex numbers), and multiplied together. Vector addition maps any pair of vectors onto another vector, specifically, the one you get by moving the second vector so that it's tail coincides with the tip of the first, without altering the length or direction of either, and then joining the tail of the first to the tip of the second. This addition rule is known as the parallelogram law. So, for example, adding vectors |A> and |B> yields vector |C> (= |A> + |B>) as in Figure 1:
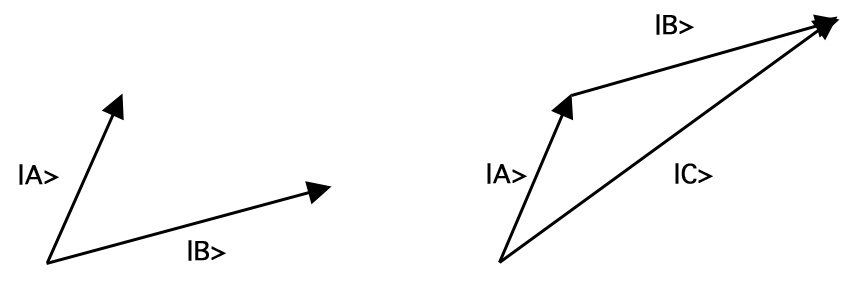
Figure 1: Vector Addition
Multiplying a vector |A> by n, where n is a constant, gives a vector which is the same direction as |A> but whose length is n times |A>'s length.
In a real vector space, the (inner or dot) product of a pair of vectors |A> and |B>, written ‘<A|B>’ is a scalar equal to the product of their lengths (or ‘norms’) times the cosine of the angle, 
, between them:
<A|B> = |A| |B| cos
Let |A1> and |A2> be vectors of length 1 ("unit vectors") such that <A1|A2> = 0. (So the angle between these two unit vectors must be 90 degrees.) Then we can represent an arbitrary vector |B> in terms of our unit vectors as follows:
|B> = b1|A1> + b2|A2>
For example, here is a graph which shows how |B> can be represented as the sum of the two unit vectors |A1> and |A2>:
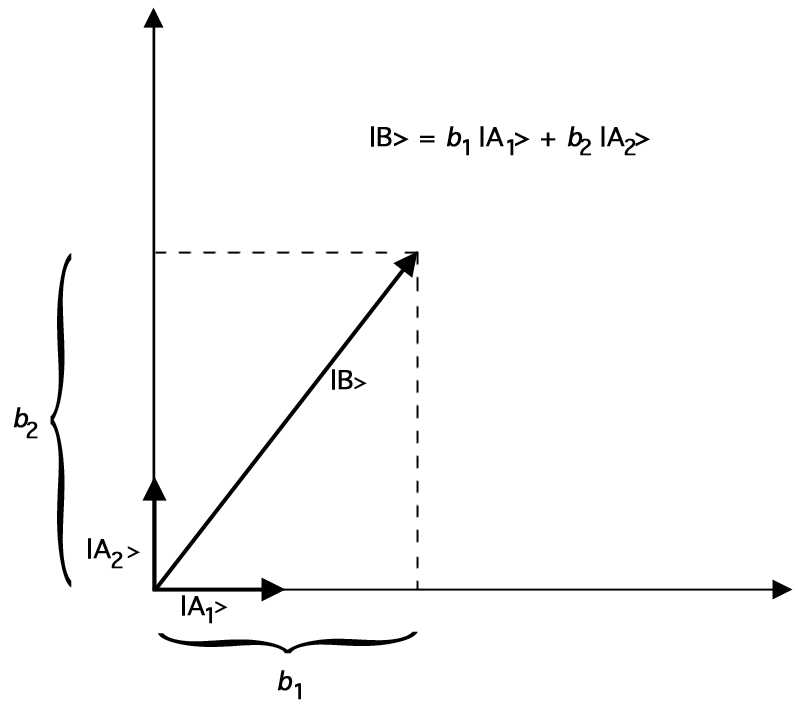
Figure 2: Representing |B> by Vector Addition of Unit Vectors
Now the definition of the inner product <A|B> has to be modified to apply to complex spaces. Let c* be the complex conjugate of c. (When c is a complex number of the form a ± bi, then the complex conjugate c* of c is defined as follows:
[a + bi]* = a 
bi
[a bi]* = a + bi
So, for all complex numbers c, [c*]* = c, but c* = c just in case c is real.) Now definition of the inner product of |A> and |B> for complex spaces can be given in terms of the conjugates of complex coefficients as follows. Where |A1> and |A2> are the unit vectors described earlier, |A> = a1|A1> + a2|A2> and |B> = b1|A1> + b2|A2>, then
<A|B> = (a1*)(b1) + (a2*)(b2)
The most general and abstract notion of an inner product, of which we've now defined two special cases, is as follows. <A|B> is an inner product on a vector space V just in case
(i) <A|A> = |A|2, and <A|A>=0 if and only if A=0
(ii) <B|A> = <A|B>*
(iii) <B|A+C> = <B|A> + <B|C>.
It follows from this that
(i) the length of |A> is the square root of inner product of |A> with itself, i.e.,
|A| = 
<A|A>,
and
(ii) |A> and |B> are mutually perpendicular, or orthogonal, if, and only if, <A|B> = 0.
A vector space is a set of vectors closed under addition, and multiplication by constants, an inner product space is a vector space on which the operation of vector multiplication has been defined, and the dimension of such a space is the maximum number of nonzero, mutually orthogonal vectors it contains.
Any collection of N mutually orthogonal vectors of length 1 in an N-dimensional vector space constitutes an orthonormal basis for that space. Let |A1>, ... , |AN> be such a collection of unit vectors. Then every vector in the space can be expressed as a sum of the form:
|B> = b1|A1> + b2|A2> + ... + bN|AN>,
where bi = <B|Ai>. The bi's here are known as B's expansion coefficients in the A-basis.[5]
Notice that:
(i) for all vectors A, B, and C in a given space,
<A|B+C> = <A|B> + <A|C>
(ii) for any vectors M and Q, expressed in terms of the A-basis,
|M> + |Q> = (m1 + q1)|A1> + (m2 + q2)|A2> + ... + (mN + qN)|AN>,
and
<M|Q> = m1q1 + m2q2 + ... + mnqn
There is another way of writing vectors, namely by writing their expansion coefficients (relative to a given basis) in a column, like so:
|Q> = |
 |
q1
q2 |
 |
where qi = <Q|Ai> and the Ai are the chosen basis vectors.
When we are dealing with vector spaces of infinite dimension, since we can't write the whole column of expansion coefficients needed to pick out a vector since it would have to be infinitely long, so instead we write down the function (called the ‘wave function’ for Q, usually represented 
(i)) which has those coefficients as values. We write down, that is, the function:
(i) = qi = <Q|Ai>
Given any vector in, and any basis for, a vector space, we can obtain the wave-function of the vector in that basis; and given a wave-function for a vector, in a particular basis, we can construct the vector whose wave-function it is. Since it turns out that most of the important operations on vectors correspond to simple algebraic operations on their wave-functions, this is the usual way to represent state-vectors.
When a pair of physical systems interact, they form a composite system, and, in quantum mechanics as in classical mechanics, there is a rule for constructing the state-space of a composite system from those of its components, a rule that tells us how to obtain, from the state-spaces, HA and HB for A and B, respectively, the state-space -- called the ‘tensor product’ of HA and HB, and written HA
HB -- of the pair. There are two important things about the rule; first, so long as HA and HB are Hilbert spaces, HAHB will be as well, and second, there are some facts about the way HAHB relates to HA and HB, that have surprising consequences for the relations between the complex system and its parts. In particular, it turns out that the state of a composite system is not uniquely defined by those of its components. What this means, or at least what it appears to mean, is that there are, according to quantum mechanics, facts about composite systems (and not just facts about their spatial configuration) that don't supervene on facts about their components; it means that there are facts about systems as wholes that don't supervene on facts about their parts and the way those parts are arranged in space. The significance of this feature of the theory cannot be overplayed; it is, in one way or another, implicated in most of its most difficult problems.
In a little more detail: if {viA} is an orthonormal basis for HA and {ujB} is an orthonormal basis for HB, then the set of pairs (viA, ujB) is taken to form an orthonormal basis for the tensor product space HAHB. The notation viAujB is used for the pair (viA,ujB), and inner product on HAHB is defined as:[6]
<viAumB | vjAunB> = <viA | vjA> <umB | unB>
It is a result of this construction that although every vector in HAHB is a linear sum of vectors expressible in the form vAuB, not every vector in the space is itself expressible in that form, and it turns out that
(i) any composite state defines uniquely the states of its components.
(ii) if the states of A and B are pure (i.e., representable by vectors vA and uB, respectively), then the state of (A+B) is pure and represented by vAuB, and
(iii) if the state of (A+B) is pure and expressible in the form vAuB, then the states of A and B are pure, but
(iv) if the states of A and B are not pure, i.e., if they are mixed states (these are defined below), they do not uniquely define the state of (A+B); in particular, it may be a pure state not expressible in the form vAuB.
Operators
An operator O is a mapping of a vector space onto itself; it takes any vector |B> in a space onto another vector |B
> also in the space; O|B> = |B>. Linear operators are operators that have the following properties:
(i) O(|A> + |B>) = O|A> + O|B>, and
(ii) O(c|A>) = c(O|A>).
Just as any vector in an N-dimensional space can be represented by a column of N numbers, relative to a choice of basis for the space, any linear operator on the space can be represented in a column notation by N2 numbers:
O = |
|
O11
O21 |
O12
O22 |
|
where Oij = < Ai | O|Aj> and the |AN> are the basis vectors of the space. The effect of the linear operator O on the vector B is, then, given by
|
= |
|
O11
O21 |
O12
O22 |
|
� |
|
b1
b2 |
|
|
= |
|
(O11b1 + O12b2)
(O21b1 + O22b2) |
|
|
= |
(O11b1 + O12b2)|A1>
| + |
(O21b1 + O22b2)|A2> |
|
= |
|B> |
|vt
|A> + 
|B> onto the state 
